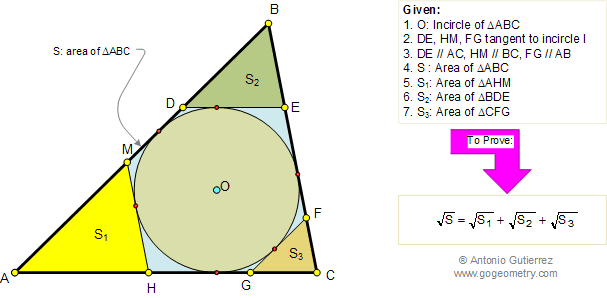
If S, S1, S2, S3 are the areas of triangles ABC, AHM, BDE,
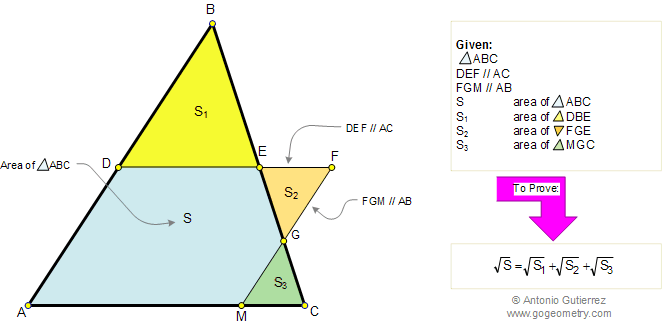
If S, S1, S2, and S3, are the areas of triangles ABC, DBE, FGE,

That is for both triangles but if we have to find the area for triangle then

Algorithms for computing area of triangles, quadrilaterals and polygons in

After looking at areas of triangles, here's the proof that Area = Base x

In all the examples above the altitude of each triangle is shown starting

into two triangles, find the area of each triangle as above,

If you regard a triangle as a rectangle or parallelogram cut in half along a

Hence it is enough to show that the sum of the areas of triangles DEA and
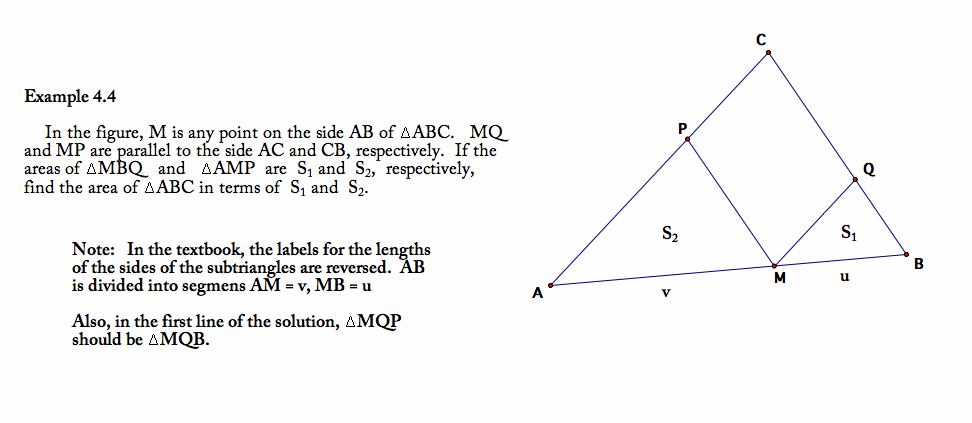
Let S be the area of triangle ABC. OBSERVE THAT THE AREA OF THE

Given triangle ACE, let's first look at the areas of triangles AHF and EHF.
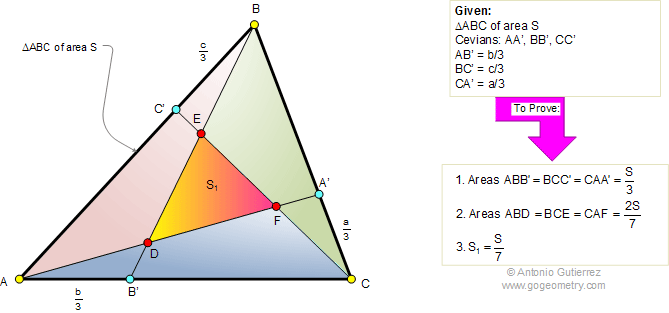
Triangle area, cevian, trisector
of triangles, quadrilaterals, and circles; and the calculation of area

three parts: the area of triangle DAP1 that is still consumer surplus;

Another property is that the area of any triangle equals one-half the height
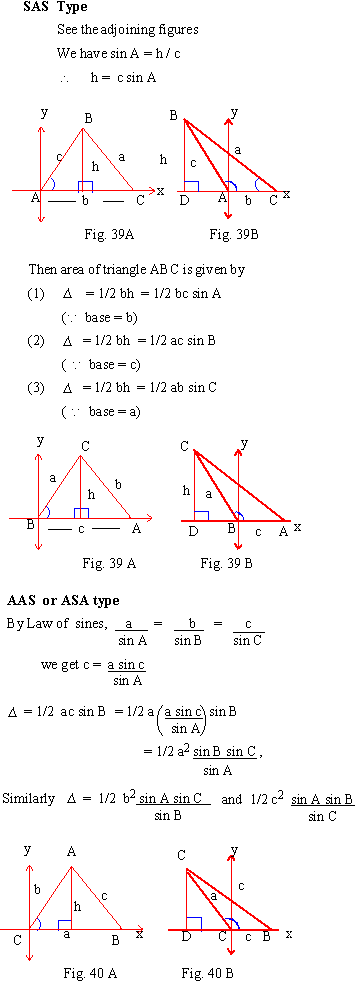
For finding the area of a triangle (D ) three types of additonal formulas
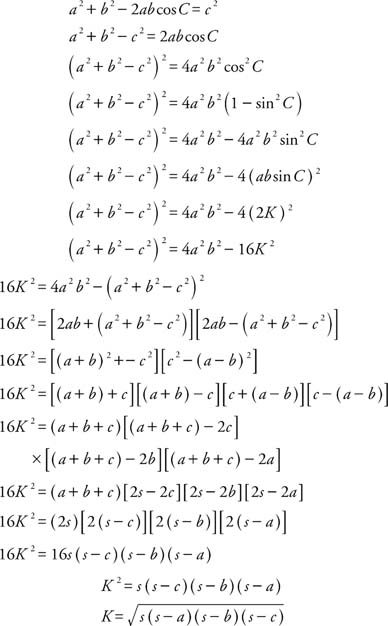
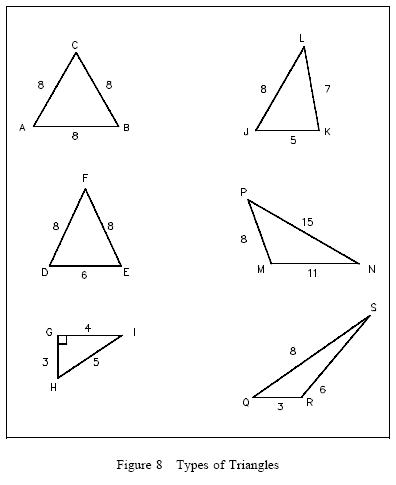
Areas of Triangles

Then, by computing the area of each triangle and trapezoid and determining

Our goal here is to prove that the area of triangles X and Y are not equal.

Recall that the area of a triangle of height h and base w is (1/2)(h•w).



